[비트코인 암호학] 1.3 타원곡선의 점 덧셈2
[비트코인 암호학] 1.2 타원곡선의 점 덧셈1 [비트코인 암호학] 1.1 타원곡선 [비트코인 암호학] 0. 비트코인의 거래와 서명 비트코인 블록체인에서 하나의 블록을 단순하게 표현하면 다음과 같습
kwjdnjs.tistory.com
지금까지 알아본 타원곡선은 실수체에서의 타원곡선이었습니다. ECDSA는 유한체에서의 타원곡선을 사용합니다. 따라서 유한체에 대해 알아야 합니다.
유한체에 대해 알아보기 전에 먼저 '체'에 대해 알아보겠습니다. 체란 집합의 원소를 사용하여 사칙연산한 결괏값이 해당 집합에 속하는 집합을 말합니다. 실수 집합의 경우 사칙연산한 결과 값이 다시 실수로 나오기 때문에 체를 이룹니다. 하지만 정수의 경우 나누어 떨어지지 않는 값들은 정수로 표현할 수 없기 때문에 체를 이루지 않습니다.
유한체는 이렇게 체를 이루지 않는 정수를 사용해 만들어진 유한집합입니다. 집합의 원소의 개수는 소수(Prime number) p의 거듭제곱입니다.(비트코인에서는 p를 거듭제곱이 아닌 소수만 사용합니다.) 그리고 이 p를 위수(order)라고 합니다. 예를 들어 위수 7의 유한체는 다음과 같습니다.

체의 정의에 의해 집합의 원소를 사용하여 사칙연산을 한 결과 값은 집합 내의 원소가 되어야 합니다. 따라서 유한체의 원소를 사용한 사칙연산의 경우 기존의 방식과 다른 새로운 방식을 사용해야 합니다. 새로운 방식에 대한 아이디어는 바로 나머지 연산입니다. 예를 들어 어떤 정수를 7로 나눈 나머지는 나누어 떨어진 경우 0, 그 외의 경우 나머지 1~6을 갖습니다. 이는 위수 7의 유한체의 원소와 같습니다.
나머지 연산은 modulo이며 mod로 사용합니다. 15를 7로 나눈 나머지를 구하는 경우 다음과 같이 표현합니다.

이를 활용하면 유한체의 덧셈을 정의할 수 있습니다. 예를 들어 위수 7의 유한체의 원소 5와 6을 더하는 경우 다음과 같이 두 값을 더한 후 위수인 7로 나눈 나머지를 구하면 됩니다.

4는 유한체의 원소이므로 유한체에서의 덧셈이 정상적으로 되었음을 알 수 있습니다. 이 과정을 일반화 하면 다음과 같이 위수 p의 유한체에서 원소 a와 b를 더하는 방식을 정의할 수 있습니다. 이 글에서는 유한체의 덧셈을 표시하기 위해 연산자에 괄호를 사용하였습니다.

뺄셈의 경우에도 같은 방식을 적용할 수 있습니다.

곱셈과 거듭제곱도 비슷한 방식을 적용할 수 있습니다.

하지만 유한체의 나눗셈은 지금까지의 방식으로는 정의할 수 없습니다. 나눗셈은 곱셈의 역연산입니다. 즉, 다음과 같이 표현할 수 있습니다.

유한체에서의 나눗셈은 위와 같이 a값을 모르는 상태에서 k와 b 그리고 p의 값을 이용하여 a값을 구하는 것입니다. 이를 위해 페르마의 소정리(Fermat's little theorem)를 사용하겠습니다. 페르마의 소정리를 지금까지 사용한 표현방식을 사용하여 표현하면 다음과 같습니다.

위 식은 p가 소수일 때 만족합니다. 지금까지 위수 p를 소수로 한정하였기 때문에 페르마의 소정리를 이용하면 다음과 같은 식을 얻을 수 있습니다.
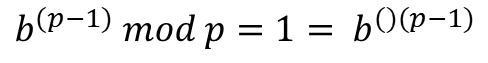
구하고자 하는 나눗셈 유한체의 나눗셈 연산식은 다음과 같이 곱셈식으로 변경할 수 있습니다.

이때 아래 식에서 나머지 연산의 분배법칙을 적용하면

아래 식이 되므로
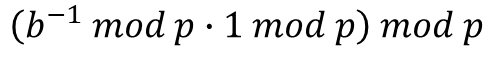
아래 식을 만족하게 되고

이 식을 페르마의 소정리를 통해 얻은 식을 사용하여 정리하면 다음과 같습니다.

위 식을 다시 정리하면

즉, 다음과 같은 결과를 얻게 됩니다.

이 결과를 나눗셈을 곱셈으로 표현한 식에 대입하면 다음과 같습니다.

이 식을 풀어서 쓰게 되면 다음과 같은 식을 얻을 수 있습니다.

이때 k 값은 다음과 같이 나머지 연산의 결과여서 유한체의 원소이므로

다음과 같은 식이 성립함을 알 수 있습니다.

이를 식에 대입하여 정리하면 최종적으로 다음과 같은 식을 얻을 수 있습니다.

최종적으로 유한체에서의 나눗셈은 다음과 같이 정리할 수 있습니다.
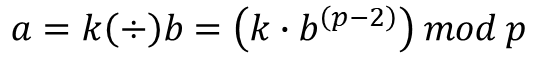
지금까지 유한체와 유한체에서의 연산에 대해 알아봤습니다. 다음 글에서는 유한체에서의 타원곡선에 대해 알아보겠습니다.
[비트코인 암호학] 2.2 유한체에서의 타원곡선
먼저 지금까지 알아봤던 내용을 정리해보겠습니다. 1. 타원곡선의 점 덧셈 다음과 같은 타원곡선과 두 점 A와 B가 존재할 때, 타원곡선의 점 덧셈은 크게 4가지 경우로 나눌 수 있었습니다. (1)
kwjdnjs.tistory.com
'비트코인 > 암호학' 카테고리의 다른 글
| [비트코인 암호학] 2.3 타원곡선의 스칼라 곱셈 (0) | 2022.07.16 |
|---|---|
| [비트코인 암호학] 2.2 유한체에서의 타원곡선 (0) | 2022.07.14 |
| [비트코인 암호학] 1.3 타원곡선의 점 덧셈2 (0) | 2022.07.08 |
| [비트코인 암호학] 1.2 타원곡선의 점 덧셈1 (0) | 2022.07.07 |
| [비트코인 암호학] 1.1 타원곡선 (0) | 2022.07.06 |