[비트코인 암호학] 1.1 타원곡선
[비트코인 암호학] 0. 비트코인의 거래와 서명 비트코인 블록체인에서 하나의 블록을 단순하게 표현하면 다음과 같습니다. 각 블록들은 이전 블록의 해시와 거래 내역을 담고 있습니다. 거래
kwjdnjs.tistory.com
이전 글에서 타원곡선에 대해 알아봤습니다. 이번 글에서는 타원곡선에서 정의된 점 덧셈에 대해 알아보겠습니다. 먼저 타원곡선 상의 두 점 A와 B가 존재한다고 가정해보겠습니다.

점 덧셈을 하기 위해 먼저 두 점 A와 B를 지나는 직선을 그립니다. 그리고 해당 직선이 점 A, B가 아니면서 타원곡선과 만나는 점 C를 찾습니다.
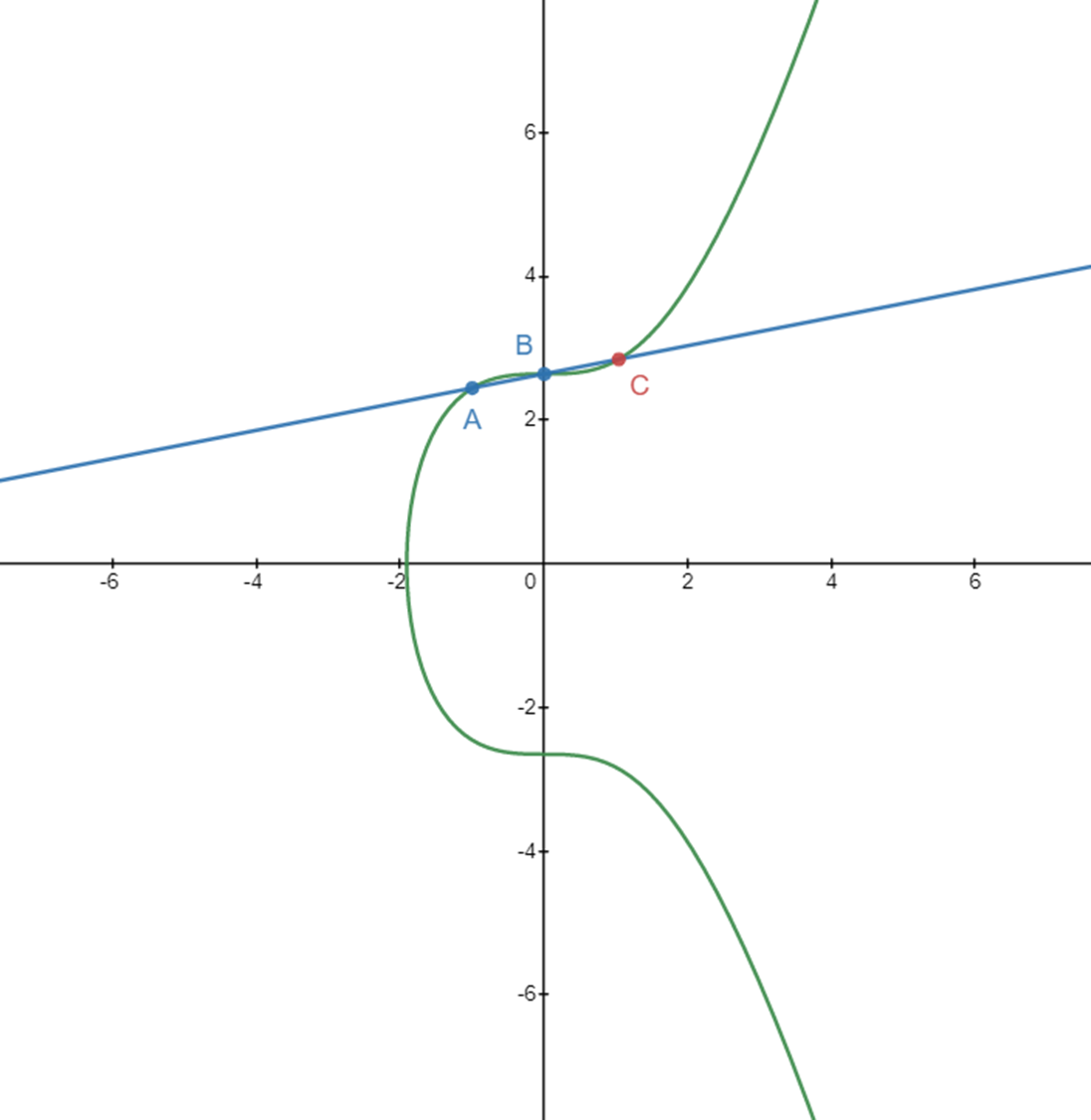
이렇게 구한 점 C의 x축 대칭인 점을 찾습니다.

최종적으로 구해진 점 -C가 바로 점 A와 B의 점 덧셈 값입니다. 이를 다음과 같이 표현할 수 있습니다.

C의 x축 대칭인 점이 -C인 이유는 점 덧셈의 규칙을 만족해야 하기 때문입니다. 예를 들어 점 A와 B가 다음과 같이 서로 x축 대칭인 점이라고 가정해보겠습니다.
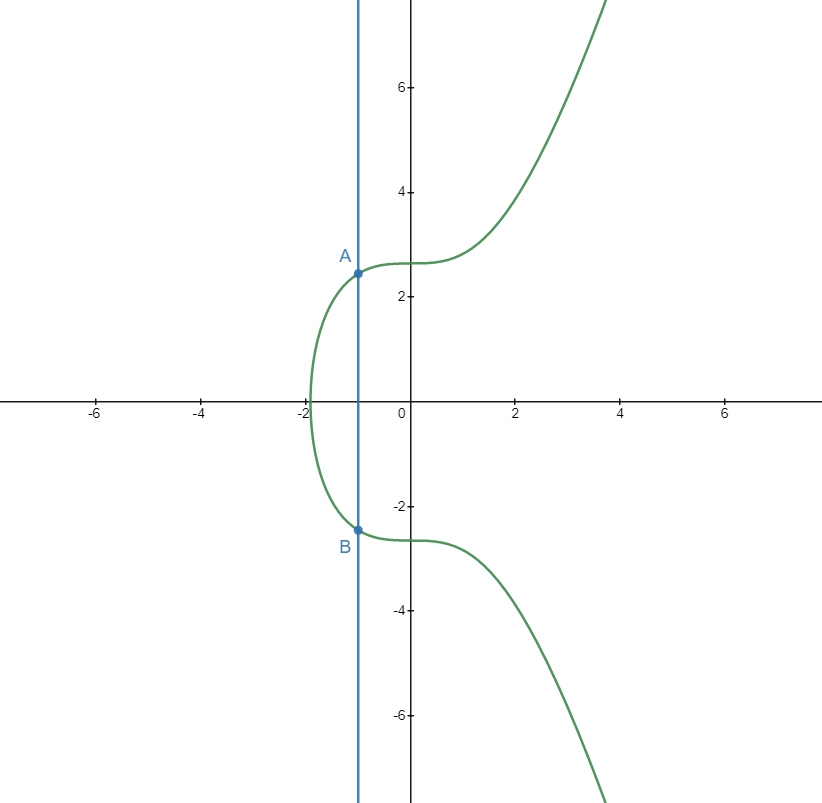
이때 A+B를 구해보려고 하면 결과가 존재할 수 없는 것처럼 보입니다. 이 경우 A와 B를 지나는 직선이 A와 B가 아니면서 타원곡선과 만나는 점을 무한원점(Point at infinity)이라고 합니다. 간단하게 0으로 표현하겠습니다.

결론적으로 B는 -A가 됩니다. 이를 이용하면 C의 x축 대칭점이 -C인 이유를 쉽게 알 수 있습니다.
지금까지 타원곡선의 점 덧셈이 어떻게 이뤄지는지 알아봤습니다. 다음 내용에서는 실제로 타원곡선의 두 점을 이용해 점 덧셈을 하기위한 공식을 유도해보겠습니다.
[비트코인 암호학] 1.3 타원곡선의 점 덧셈2
이번 글에서는 타원곡선의 점 덧셈을 공식화해보겠습니다. 먼저 타원곡선의 점 덧셈에서 나타날 수 있는 경우를 크게 4가지로 나눠보겠습니다. 1. 점 A와 B가 서로 x축 대칭인 경우 2. 점 A와 B가
kwjdnjs.tistory.com
'비트코인 > 암호학' 카테고리의 다른 글
| [비트코인 암호학] 2.2 유한체에서의 타원곡선 (0) | 2022.07.14 |
|---|---|
| [비트코인 암호학] 2.1 유한체 (0) | 2022.07.11 |
| [비트코인 암호학] 1.3 타원곡선의 점 덧셈2 (0) | 2022.07.08 |
| [비트코인 암호학] 1.1 타원곡선 (0) | 2022.07.06 |
| [비트코인 암호학] 0. 비트코인의 거래와 서명 (0) | 2022.07.06 |