[비트코인 암호학] 1.2 타원곡선의 점 덧셈1
[비트코인 암호학] 1.1 타원곡선 [비트코인 암호학] 0. 비트코인의 거래와 서명 비트코인 블록체인에서 하나의 블록을 단순하게 표현하면 다음과 같습니다. 각 블록들은 이전 블록의 해시와 거
kwjdnjs.tistory.com
이번 글에서는 타원곡선의 점 덧셈을 공식화해보겠습니다. 먼저 타원곡선의 점 덧셈에서 나타날 수 있는 경우를 크게 4가지로 나눠보겠습니다.
1. 점 A와 B가 서로 x축 대칭인 경우
2. 점 A와 B가 서로 x축 대칭이 아니면서 다른 점일 경우
3. 점 A와 B가 같은 점일 경우
4. 점 A와 B가 같은 점이면서 점의 y좌표가 0인 경우
1. 점 A와 B가 서로 x축 대칭인 경우
먼저 1번의 경우는 이전 글에서 이미 다뤘습니다.

점 A와 B가 서로 x축 대칭인 경우 점 덧셈한 값은 무한원점이 됩니다.

2. 점 A와 B가 서로 x축 대칭이 아니면서 다른 점일 경우
이어서 2번의 경우를 보겠습니다. 2번의 경우는 다음과 같이 A와 B가 서로 다른 점일 경우입니다.

이 경우 점 A와 B를 이은 직선이 타원곡선과 만나는 다른점 C를 x축 대칭이동한 값이 점 덧셈의 결과가 되었습니다.

이를 실제로 계산해보겠습니다.
먼저 점 A를 (x1, y1) 점 B를 (x2, y2)라고 해보겠습니다. 그러면 이전에 다뤘던 비트코인의 타원곡선 방정식과 함께 다음과 같이 정리할 수 있습니다.

여기에서 점 C를 먼저 구해보겠습니다. 점 C를 구하기 위해선 먼저 점 A와 B를 지나는 직선의 방정식을 구해야 합니다. 직선의 방정식을 구하기 위해 먼저 기울기 m을 구합니다. 기울기 m은 다음과 같이 두 점을 통해 쉽게 구할 수 있습니다.

직선은 점 A를 지나기 때문에 직선의 방정식을 다음과 같이 정리할 수 있습니다.

이때 점 C는 다음과 같이 타원곡선의 방정식과 직선의 방정식을 모두 만족해야 합니다.

따라서 점 C를 구하기 위해 타원곡선의 방정식에 직선의 방정식을 대입하겠습니다.

위 식을 정리하면 다음과 같습니다.

이때 점 C를 x3, y3라고 하겠습니다.
해당식(식1)을 만족하는 x값은 모두 x1, x2, x3이기 때문에 삼차방정식인 해당식은 다음과 같이 정리될 것입니다.

이 식을 전개하면 다음과 같습니다.

첫 번째 식(식1)과 두 번째 식(식2)은 같은 식이기 때문에 근과 계수와의 관계에 의해 값 x3를 구하기 위해 다음과 같이 정리할 수 있습니다.
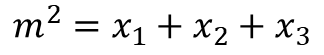
이를 x3에 대해 정리하면 다음과 같습니다.

점 C는 직선의 방정식을 만족하기 때문에 직선의 방정식에 x3를 대입해 다음과 같이 y3를 구할 수 있습니다.

결론적으로 서로 다른 점 A와 B의 점 덧셈 결과는 다음과 같이 점 A와 B를 이용해 기울기를 구한 후

이 값을 이용해 x3와 y3를 계산합니다.


점 덧셈의 결과는 점 C의 x축 대칭 값 즉, -C 이므로 최종적으로 다음과 같은 결과를 가지게 됩니다.

3. 점 A와 B가 같은 점일 경우
다음은 점 A와 B가 같은 점일 경우입니다. 쉽게 이해하기 위해 이전에 알아봤던 점 A와 B가 서로 다른 점인 상황에서 점 B를 점 A 쪽으로 계속 이동시켜서 같게 만들어 보겠습니다.

그 결과 A와 B가 같은 경우 점 A에서의 접선이 타원곡선과 만나는 점 C의 x축 대칭점이 점 덧셈 값임을 알 수 있습니다. 접선의 기울기는 미분을 사용하여 다음과 같이 구할 수 있습니다.

즉, 점 A에서의 기울기는 다음과 같습니다.

또한 A와 B가 다른 점일 경우에 구했던 식에 x2 대신 x1을 대입하여 다음과 같이 점 덧셈 결과를 구할 수 있습니다.

4. 점 A와 B가 같은 점이면서 점의 y좌표가 0인 경우
마지막으로 4번의 경우입니다. 그래프를 그려보면 어떠한 상황인지 쉽게 알 수 있습니다.

이 경우 점 덧셈 결과 값은 1번의 경우처럼 무한원점이 됩니다.
지금까지 총 4가지 경우에서의 점 덧셈을 구하는 공식에 대해 알아봤습니다. 다음 글에서는 유한체에서의 점 덧셈을 하기 위해 유한체에 대해 알아보겠습니다.
[비트코인 암호학] 2.1 유한체
지금까지 알아본 타원곡선은 실수체에서의 타원곡선이었습니다. ECDSA는 유한체에서의 타원곡선을 사용합니다. 따라서 유한체에 대해 알아야 합니다. 유한체에 대해 알아보기 전에 먼저 '체'
kwjdnjs.tistory.com
'비트코인 > 암호학' 카테고리의 다른 글
| [비트코인 암호학] 2.2 유한체에서의 타원곡선 (0) | 2022.07.14 |
|---|---|
| [비트코인 암호학] 2.1 유한체 (0) | 2022.07.11 |
| [비트코인 암호학] 1.2 타원곡선의 점 덧셈1 (0) | 2022.07.07 |
| [비트코인 암호학] 1.1 타원곡선 (0) | 2022.07.06 |
| [비트코인 암호학] 0. 비트코인의 거래와 서명 (0) | 2022.07.06 |