[비트코인 암호학] 2.2 유한체에서의 타원곡선
[비트코인 암호학] 2.1 유한체 [비트코인 암호학] 1.3 타원곡선의 점 덧셈2 [비트코인 암호학] 1.2 타원곡선의 점 덧셈1 [비트코인 암호학] 1.1 타원곡선 [비트코인 암호학] 0. 비트코인의 거래와 서명
kwjdnjs.tistory.com
이전 글에서 유한체의 타원곡선의 점 덧셈에 대해 알아봤습니다. 해당 내용을 정리하면 다음과 같습니다.
(1)


(2)


(3)

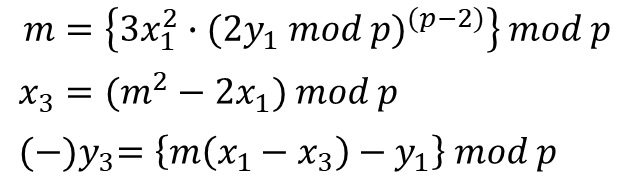
(4)


이를 이용하면 유한체 타원곡선의 스칼라 곱셈을 정의할 수 있습니다. 곱셈은 기본적으로 어떠한 수를 여러 번 더하는 것입니다. 예를 들어 3을 세 번 더한 3+3+3은 3x3으로 표현할 수 있습니다. 이와 비슷하게 점 덧셈에서도 여러 번 반복해서 점 덧셈하는 것을 스칼라 값과의 곱으로 표현할 수 있습니다. 이를 수식으로 표현하면 다음과 같습니다.

만약 A를 n번 더한다면 다음과 같이 표현할 수 있습니다.

실제로 스칼라 곱셈을 해보겠습니다. 먼저 다음과 같이 타원곡선의 방정식과 위수 p가 주어진 상태에서 점 A를 선정하겠습니다.

그리고 점 A를 곱해보겠습니다.

위 스칼라 곱셈 결과처럼 어떤 점 A에 대하여 점 덧셈을 반복하면 무한원점에 도달하게 되고, 이후에는 이전 점 덧셈 결과가 반복되어 나타납니다. 따라서 점 A에 대해 다음과 같은 '군'을 얻을 수 있습니다.

이를 일반화 하여 표현하면 다음과 같이 점 G에 대한 군으로 표현할 수 있습니다.

여기서의 n값을 군의 위수라고 합니다.
지금까지 ECDSA를 위한 기본적인 도구를 모두 다뤘습니다. 이 도구들을 모두 정리하면 다음과 같습니다.

- a와 b는 타원곡선 방정식의 값으로 지금까지 a=0, b=7을 사용했습니다.
- p는 유한체의 위수입니다.
- G는 타원곡선 위의 한 점입니다.
- n은 점 G의 군에 대한 위수입니다.
이어지는 글들에서는 secp256k1에서 미리 정의된 위 변수들의 값을 이용해 공개키와 개인키를 생성하여 디지털 서명을 하고 검증하는 내용을 다루게 됩니다. 이를 위해 다음 글에서는 공개키 암호화에 대해 먼저 다루겠습니다.
[비트코인 암호학] 3.1 공개키 암호화
타원곡선을 이용해 디지털 서명을 하고 검증하기 위해서는 공개키(Public key)와 개인키(Private key)가 필요합니다. 공개키와 개인키로 디지털 서명을 하는 방법에 대해 설명하기 전에 먼저 공개키
kwjdnjs.tistory.com
'비트코인 > 암호학' 카테고리의 다른 글
| [비트코인 암호학] 3.2 공개키와 개인키 (0) | 2022.07.20 |
|---|---|
| [비트코인 암호학] 3.1 공개키 암호화 (0) | 2022.07.18 |
| [비트코인 암호학] 2.2 유한체에서의 타원곡선 (0) | 2022.07.14 |
| [비트코인 암호학] 2.1 유한체 (0) | 2022.07.11 |
| [비트코인 암호학] 1.3 타원곡선의 점 덧셈2 (0) | 2022.07.08 |