이번 글에서는 이전 글에서 생성했던 서명을 검증해보겠습니다.
[비트코인 암호학] 4.2 ECDSA - 1
지금까지 알아봤던 내용들을 정리해보겠습니다. 먼저 타원곡선과 점 덧셈 그리고 유한체 타원곡선과 스칼라 곱셈에 대해 살펴봤습니다. 이후 이 내용들을 토대로 다음과 같이 secp256k1에서 정
kwjdnjs.tistory.com
A는 다음과 같이 개인키 d, 무작위 값 k, 메시지의 해시값인 z, 생성점 G를 이용해 서명 (r, s)를 생성하여 공개키 P와 메시지 m과 함께 B에게 전송했습니다.

B는 전달받은 값을 이용해 서명을 검증할 수 있습니다. 먼저 다음 식을 다시 한번 생각해 보겠습니다.
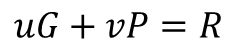
이전에 알아봤던 것처럼 위 식은 공개된 G, P, R을 이용해 다양한 u와 v값 조합을 가질 수 있습니다. 이 중 아래의 u와 v의 조합은 오직 A만 생성할 수 있었습니다.
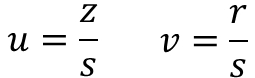
그 이유는 다음과 같이 값 s가 A만 알고 있는 값인 개인키 d와 비공개된 무작위 값인 k를 포함하고 있기 때문입니다.
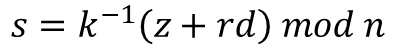
결론적으로 B는 전송받은 r과 s 그리고 메시지의 해시값인 z를 이용해 u와 v를 구하고 G, P, R에 대한 식에 대입해 식이 올바른지 확인하는 것으로 서명을 검증할 수 있습니다. 만약 누군가가 올바르지 않은 개인키 d 또는 올바르지 않은 무작위 값 k를 이용해 s를 계산해 전송했다면, 공개키 P를 포함한 G, P, R에 대한 식을 만족하지 못할 것이기 때문입니다.
지금부터는 실제로 서명을 검증해보겠습니다. 먼저 전달받은 메시지 m의 해시값 z를 구합니다. 그리고 서명 (r, s)를 이용해 u와 v를 구합니다. u와 v는 G의 군의 위수인 n을 기준으로 순환하기 때문에 계산 과정에서 위수인 n으로 나눈 나머지를 구합니다. 이를 위해 먼저 1/s를 계산해줍니다.
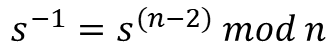
위 값을 대입하여 u와 v를 구합니다.
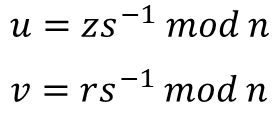
이 값을 G, P, R에 대한 식에 대입해 u와 v 값이 올바른지 확인합니다.
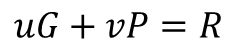
만약 식이 올바르게 계산된다면 전송받은 서명은 올바른 서명임을 알 수 있습니다.
지금까지 ECDSA에 대한 모든 내용을 다뤘습니다. 타원곡선을 이용해 개인키에서 공개키를 생성했으며, 이를 이용해 디지털 서명을 생성하고 검증했습니다. 비트코인은 물론 이더리움에서도 사용되는 이러한 서명 방식을 이해하면, 블록체인에서 거래를 어떻게 서명하고 전송하는지에 대해 이해할 수 있습니다.
지금까지의 글들이 ECDSA를 이해하는데 도움이 되었다면 좋겠습니다. 감사합니다.
이어지는 글
[비트코인 코드] 개인키(Private key), 공개키(Public key), 주소(Address) 생성
미리 알아야 할 내용들 '비트코인/암호학' 카테고리의 글 목록 평범한 대학생의 블록체인 기술 관련 블로그 입니다. kwjdnjs.tistory.com [비트코인 암호학] 3.1 공개키 암호화 타원곡선을 이용해 디
kwjdnjs.tistory.com
[비트코인 암호학] 5. 슈노르 서명(Schnorr signature)
[비트코인 암호학] 3.2 공개키와 개인키 [비트코인 암호학] 3.1 공개키 암호화 [비트코인 암호학] 2.3 타원곡선의 스칼라 곱셈 [비트코인 암호학] 2.2 유한체에서의 타원곡선 [비트코인 암호학] 2.1 유
kwjdnjs.tistory.com
'비트코인 > 암호학' 카테고리의 다른 글
| [비트코인 암호학] 5. 슈노르 서명(Schnorr signature) (0) | 2023.01.16 |
|---|---|
| [비트코인 암호학] 4.2 ECDSA - 1 (0) | 2022.07.23 |
| [비트코인 암호학] 4.1 디지털 서명 (0) | 2022.07.21 |
| [비트코인 암호학] 3.2 공개키와 개인키 (0) | 2022.07.20 |
| [비트코인 암호학] 3.1 공개키 암호화 (0) | 2022.07.18 |