[비트코인 암호학] 4.1 디지털 서명
[비트코인 암호학] 3.2 공개키와 개인키 [비트코인 암호학] 3.1 공개키 암호화 [비트코인 암호학] 2.3 타원곡선의 스칼라 곱셈 [비트코인 암호학] 2.2 유한체에서의 타원곡선 [비트코인 암호학] 2.1 유
kwjdnjs.tistory.com
지금까지 알아봤던 내용들을 정리해보겠습니다. 먼저 타원곡선과 점 덧셈 그리고 유한체 타원곡선과 스칼라 곱셈에 대해 살펴봤습니다. 이후 이 내용들을 토대로 다음과 같이 secp256k1에서 정의된 변수들에 대해서도 살펴봤습니다.
- 타원곡선 방정식의 a = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
- 타원곡선 방정식의 b = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000007
- 유한체의 위수 p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
- 생성점 G의 x좌표 = 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
- 생성점 G의 y좌표 = 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
- G의 군의 위수 n = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
그리고 생성점 G와 개인키 d로 타원곡선의 스칼라 곱셈을 이용해 다음과 같이 공개키 P를 구했습니다.

이번 글에서는 이러한 내용들을 이용한 ECDSA에 대해 알아보겠습니다. ECDSA는 Elliptic Curve Digital Signature Algorithm의 약자로 번역하면 타원곡선 디지털 서명 알고리즘입니다. 이전 글에서 다뤘던 디지털 서명을 타원곡선을 이용하여 구현하기 때문에 붙여진 이름입니다. 이미 타원곡선을 이용해 공개키와 개인키를 생성하였으므로, 이 값들을 이용해 디지털 서명을 해보겠습니다.
먼저 디지털 서명을 위해 필요한 값에 대해 알아보겠습니다. 이전에 디지털 서명에 대해서 다뤘던 내용에서 A가 B에게 전송해야 될 내용은 다음과 같이 A의 공개키와 원본 메시지 그리고 암호화된 메시지였습니다.
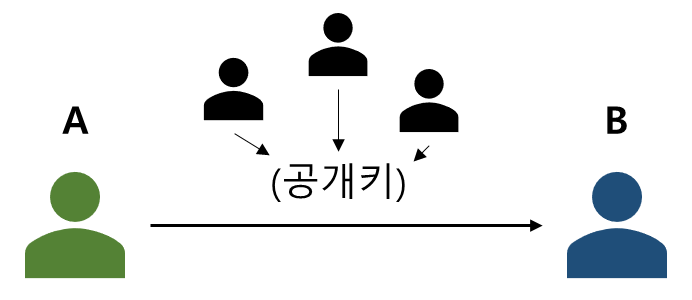

ECDSA에서는 다음과 같이 메시지 m과 해시 함수를 통해 변환된 메시지 z, 생성점 G와 무작위 값인 k 그리고 개인키 d를 이용해 암호화된 메시지인 서명 (r, s)을 구한 후, 메시지 m과 공개키 P, 서명인 r과 s를 상대방에게 넘겨주게 됩니다.

공개키 P와 메시지 m은 이미 알고 있는 값이므로, 서명 함수를 통해 구해야 하는 값인 r과 s를 메시지 m의 해시값 z와 개인키 d 그리고 무작위 값인 k를 이용해 구해보겠습니다.
먼저 r을 구해보겠습니다. r은 매번 무작위로 결정되는 수 k를 생성점 G에 스칼라 곱셈한 값 R의 x좌표입니다. 여기에서 k는 1부터 G의 군의 위수인 n보다 1 작은 값 사이 즉, 1 ~ n-1 범위의 값으로 결정됩니다.

이렇게 구한 r값을 이용하여 s값을 구해보겠습니다. 먼저 다음식에 대해 생각해보겠습니다.

생성점 G와 공개키 P 그리고 R은 모두에게 공개된 값입니다. R의 경우 x좌표인 r을 전송하는 것이지만, 이 값을 타원곡선에 대입하면 y의 값을 구할 수 있기 때문에 공개된 값으로 볼 수 있습니다. u와 v는 해당 식을 만족하는 값으로 어떤 특정한 값입니다. 즉, u와 v를 모르는 상황에서 위 식에 값을 무작위로 대입하여 정해진 u와 v의 조합을 찾는 것은 쉽지 않습니다. 따라서 올바른 u와 v 값을 전송한 사람은 u와 v의 값을 계산하여 구했다는 것을 알 수 있습니다. u와 v를 찾도록 도와줄 값 s를 구하기 위해 다음과 같이 식을 정리해보겠습니다.
먼저 P와 R에 대한 식을


u와 v에 대한 식에 대입합니다.

그리고 이 식을 정리하면 다음과 같습니다.

그리고 해당 식이 메시지 m의 해시값인 z를 포함하도록 u와 v를 정의합니다.

이 값을 식에 대입하여 정리하면 다음과 같이 값 s를 구할 수 있습니다.

값 u와 v는 G의 군의 위수인 n에 의해 순환하기 때문에 s를 구하는 과정에서 유한체에서의 계산처럼 위수 n으로 나눈 나머지를 계산합니다. 우선 이전 글에서 알아봤던 유한체에서의 나눗셈을 이용해 1/k를 구해줍니다.

그다음 값을 식에 대입합니다. 아래의 식이 값 s를 구하는 최종 식입니다.

결론적으로 개인키 d를 가진 사람은 무작위 값 k를 생성해 r을 구하여 해시값 z와 개인키 d를 이용해 s를 구할 수 있습니다.
최종적으로 전송하는 값은 공개키 P와 서명 (r, s) 그리고 메시지 값 m입니다. 이에 대해 조금 더 깊게 생각해보면 무작위 값 k를 이용하는 이유를 알 수 있습니다. 전송된 r과 s 그리고 메시지 값 m을 이용하면 누구나 쉽게 u와 v를 계산할 수 있습니다. 즉 아래 식에서 u와 v는 공개된 값임을 알 수 있습니다.

이때 만약 무작위 값인 k가 공개된다면 손쉽게 개인키 d를 알아낼 수 있습니다. 하지만 k가 공개되지 않는다면 개인키 d를 알아내기 어렵습니다. 해당식을 만족하는 d와 k의 조합은 매우 많기 때문입니다. k가 공개되지 않을 경우 안전한 이유는 값 r의 생성과정을 보면 알 수 있습니다. 이전에 설명했던 것처럼 값 r은 다음과 같이 구할 수 있었습니다.
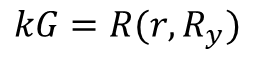
생성점 G와 값 r은 공개된 값입니다. 하지만 위 식은 타원곡선의 스칼라 곱셈 식입니다. 즉 k와 G를 이용해 r을 구하는 것은 쉽지만, G와 r을 이용해 k를 구하는 것은 어렵습니다. 이는 공개키를 생성했던 과정과 비슷합니다.

서명 생성과정을 최종적으로 정리하면 다음과 같습니다.
1. 개인키를 이용해 공개키 생성

2. 매번 변경되는 1 ~ n-1 범위의 무작위 값 k를 이용해 값 r 구하기

3. 메시지 m의 해시값 z와 개인키 d 그리고 k와 r을 이용해 s 구하기


4. 공개키 P와 서명 (r, s), 메시지 m 전송
지금까지 ECDSA 중 디지털 서명을 생성하는 과정에 대해 알아봤습니다. 다음 글에서는 전송받은 서명을 검증하는 방법에 대해 알아보겠습니다.
[비트코인 암호학] 4.3 ECDSA - 2
이번 글에서는 이전 글에서 생성했던 서명을 검증해보겠습니다. [비트코인 암호학] 4.2 ECDSA - 1 지금까지 알아봤던 내용들을 정리해보겠습니다. 먼저 타원곡선과 점 덧셈 그리고 유한체 타원
kwjdnjs.tistory.com
'비트코인 > 암호학' 카테고리의 다른 글
| [비트코인 암호학] 5. 슈노르 서명(Schnorr signature) (0) | 2023.01.16 |
|---|---|
| [비트코인 암호학] 4.3 ECDSA - 2 (0) | 2022.07.28 |
| [비트코인 암호학] 4.1 디지털 서명 (0) | 2022.07.21 |
| [비트코인 암호학] 3.2 공개키와 개인키 (0) | 2022.07.20 |
| [비트코인 암호학] 3.1 공개키 암호화 (0) | 2022.07.18 |